Making math accessible in Metanorma PDFs

Ronald Tse

Alexander Dyuzhev on 26 Aug 2021

Background

Math is a fundamental part of life — and the publication of them inside documents are too.

While math formulas are often embedded in academic papers or books published in PDF, the accessibility of those formulas is largely an ignored question.

Ever tried to copy out a math formula from a PDF? Typically the frustration cycle reads like:

Attempt to highlight the math formula with a horizontal selection
Failing that, attempt to "block select" the math formula
Copy and pasting the selected text leads to broken Unicode symbols
Frustrated mumbling about that things do not work "out of the box" and the compromise of manually crafting that formula, again.

The Bureau International des Poids et Mesures (BIPM; English: International Bureau of Weights and Measures) is the international treaty organization that defines and manages the International System of Units, commonly called the “SI system” or the “metric system”, had exactly that need of making math formulas accessible.

In collaboration with the BIPM to publish a digitally-native, semantic version of the SI Brochure using Metanorma, one of the goals is to make math formulas published in PDF as accessible as possible.

The nearly 3,000 math formulas in the SI Brochure define the basis of the International System of Units, provide an important trove of information for scientists in their usage of units.

How Metanorma publishes math in PDF

Metanorma generates PDFs through mn2pdf, a Java PDF processor based on the open-source Apache FOP (Formatting Objects Processor), a print formatter driven by XSL formatting objects (XSL-FO) technology.

In Metanorma, math formulas are encoded in MathML v3, and then rendered in PDF using the SVG (Scalable Vector Graphics) format through the JEuclid library.

The traditional way of handling math as SVG will present a pretty rendering of math, but not necessarily reuseable:

Characters embedded in math formulas cannot be searched within PDF readers, since SVG is a vector graphics format;
Text cannot be selected from math formulas from PDF and then pasted into another destination (e.g. text editor).

Math accessibility is not currently addressed in the PDF standard suite:

ISO 32000-1:2008, the PDF 1.7 standard; or
ISO 14289-1:2014, the PDF/UA (PDF universal accessibility) standard.

Making math accessible in PDFs

In the BIPM SI Brochure we introduce several math accessibility features that allow us to bypass these restrictions.

We have to first recognize that there is a spectrum of PDF readers that offer different levels of support to PDF features, despite requirements stated in the PDF standards. While Adobe Reader generally provides good support of standard requirements and some PDF/UA features, PDF readers such as Preview or Skim may only implement a subset of the standard without PDF/UA support.

When devising these techniques, we adopt a "highest bar" approach where there is a base level of access to all, and additional accessibility features become available for PDF readers that support them.

These advanced PDF techniques include:

Embedding MathML formulas as PDF attachments;
Techniques to render AsciiMath/LaTeX Math as PDF content to allow copy/pasting for non-Adobe readers (PDF content tree)
Using PDF/UA features such as "Actual Text" and "Alternate Text" for tag readers (PDF tag tree)

These techniques developed by the Metanorma team are described below.

Technique 1: Embed MathML formulas as attachments

MathML is the the industry standard in representing math formulas, now at version 3, with version 4 in the making. MathML is an XML-based language that offers both semantic and presentation formats, where the presentation format is most commonly used.

Metanorma supports multiple math input mechanisms, including MathML, LaTeX math (Wikibooks) and AsciiMath, and standardizes on storing math in the canonical MathML format.

Interoperable re-use of math formulas can be best facilitated by offering a math formula’s MathML form from within the PDF. Since PDF supports embedding of attachment files, here we describe the technique of embedding MathML files as PDF attachments.

The established way of storing individual MathML formulas is with files that end in the .mml extension (the IANA-registered extension for MathML documents).

The general process goes like this:

For every MathML formula, we create a corresponding .mml file
In the PDF, we link every rendered math formula (which is rendered into SVG) to the corresponding .mml file as a PDF attachment.

The result is that every math formula is linked to a MathML file that includes its MathML representation.

Note	Not every PDF reader supports PDF attachments!

MathML attachments in Adobe Acrobat’s "Attachments" pane

Figure 1. MathML attachments within the PDF (Adobe Acrobat "Attachments" pane)

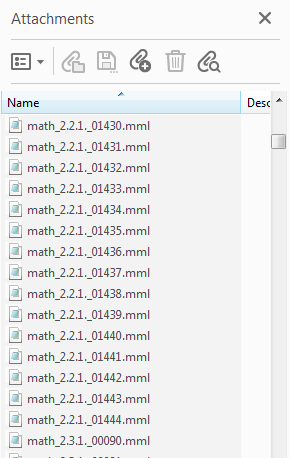
If the PDF reader (e.g. Adobe Reader DC) supports PDF attachments, a click on the math formula will open (or at least, present a prompt) the corresponding MathML file.

Figure 2. Viewing the corresponding MathML source in Notepad

Table 1. PDF attachment support in PDF readers on different platforms
Support	Platform	Application
✓	Windows	Adobe Reader
✓	macOS	Adobe Reader
✗	macOS	Preview
✗	macOS	Skim

Note

Microsoft Windows, by default, does not recognize the extension .mml mapping to the MathML format (or XML, for that matter).

When opening an .mml file for the first time, you will need to set the default application to open files with .mml extension, for example, to Notepad.

Steps to register .mml on Windows:

Find any .mml file on disk, or create an empty .mml file (for example, with the command notepad sample.mml)
Select the .mml file in Windows Explorer, right-click to open the context menu, select "Open with" and choose the desired program to open with. If the desired application is not shown, select "Choose another app". Once an application is selected, check the box next to "Always use this app to open .mml files".
Close and re-open the PDF reader application.

See this link for further information.

Technique 2: Embed human-readable math in the PDF content tree to allow copy/pasting

While MathML fully expresses the intent of a math formula, being an XML language it is not superbly readable by humans (with exceptions, of course…).

We define "human-readable math" as a math formula that can be easily typed and understood by humans, and the two leading formats are:

LaTeX math, which dictates a format that has been in use for years in the TeX ecosystem;
AsciiMath, a math representation format that only uses ASCII characters.

Both of these formats can be losslessly transformed into MathML.

For example, the "lowercase phi" (ɸ) character, of which entry would require some keystroke gymastics on a normal machine, can be represented simply with:

LaTeX math: \phi
AsciiMath: phi

Providing human-readable math in the PDF enables the following:

Finding math symbols within the PDF;
Copy/pasting and selection of math symbols from the PDF

We utilize the insight that a PDF file actually contains two types of content, the content tree and the tag tree. The content tree provides a hierarchy of data elements that represent the selectable text of a PDF file. The tag tree provides a hierarchy of data elements intended for accessibility applications.

Ever wonder how a scanned PDF file treated with OCR allows you to select text on top of a scan? That’s the PDF content tree being layered behind the scanned image.

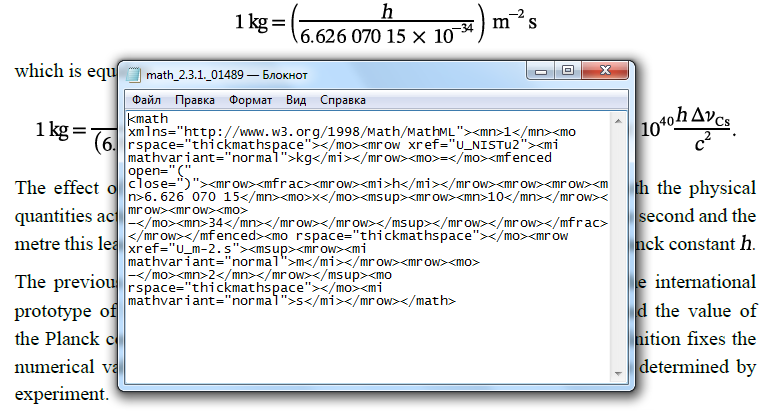
This technique involves inserting "invisible text" behind SVG math formulas. This means that we insert the human-readable math formulas in the PDF content tree, but place them "behind" the rendered math formulas so that they are still selectable.

Note	The term "behind" here refers to placing accessible text content with a lower z-index than the presentational text layer.

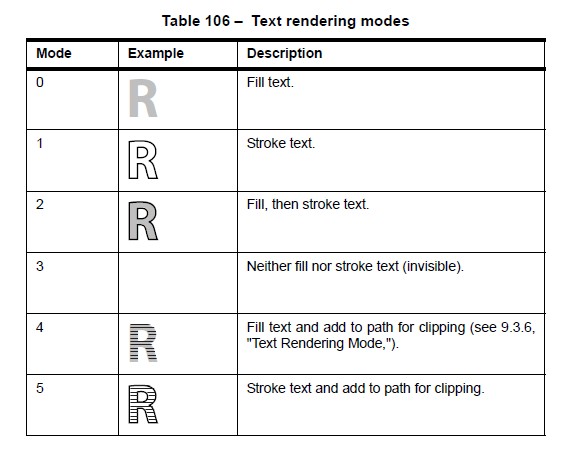
The PDF specification, ISO 32000-1:2008, 9.3.6, supports different "text rendering modes". Mode 3 is invisible text, which means that the text is rendered with no fill nor stroke. This technique is used to hide the accessible, text-selectable, math without affecting the presentation, behind the normal content.

Figure 3. ISO 32000-1:2008 supported text rendering modes

To achieve this, mn2pdf directly edits the Apache FOP Intermediate Format allowing the insertion of low-level changes within XSL-FO layout processing.

This involves the following steps:

In the data source, embed the additional human-readable math markup;

Note
In the Metanorma SI Brochure, human-readable math markup is embedded in Metanorma presentation XML as comments in the MathML <math> tag.
Determine position and bounding box (width and height) of the rendered SVG math formula;
Determine font size of the human-readable math to fit into bounding box;
Insert the human-readable math as transparent text (i.e. the text is invisible on any background) behind the rendered math formula SVG.

As shown in the screenshot below, the human-readable math markup (here AsciiMath) is inserted into the Content tree.

Human-readable math inserted into the PDF Content tree shown in Adobe Acrobat’s "Navigation > Content" pane

Figure 4. Human-readable math inserted into the PDF Content tree (Adobe Acrobat "Navigation > Content" pane)

To select the human-readable math markup of formula, the user only needs to click and drag the cursor from the left edge of the formula to its right edge. The selected text can then be copied and pasted into any application of choice.

Note	If you click on the formula, the MathML PDF attachment will be opened as per technique 1.

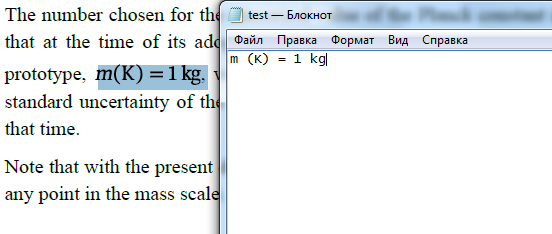
Figure 5. Human-readable math copied from PDF

Math formulas can be a lot more complex than the above sample. In the screenshot below, notice that to fully copy the human-readable math it is necessary to select the text a few characters early and then end the selection a few characters after the visible formula. This is an issue with the PDF reader’s selection implementation, but at least allows the formula to be copied out in full.

Figure 6. Complex human-readable math copied from PDF

Note	The light blue highlight at the bottom part of the rendered formula reflects where the inserted invisible text (AsciiMath) is located.

This functionality is available on most PDF readers.

Table 2. Human-readable math selection support in PDF readers on different platforms
Support	Platform	Application
✓	Windows	Adobe Reader
✓	macOS	Adobe Reader
✓	macOS	Preview
✓	macOS	Skim

Technique 3: Embed human-readable formulas for tag readers using PDF/UA features (PDF Tag tree)

The PDF standards provide two sets of accessibility mechanisms:

ISO 32000-1:2008 PDF specifies "alternate text";
ISO 14289-1:2014 PDF/UA specifies "actual text" or "replacement text".

"Alternate text" functionality is similar to the alt tag in HTML where a piece of text is used to provide human-readable information that provides an alternative representation of a content element, such as text description for a figure or a media file. This is commonly used by text-to-speech engines to vocalize text for users with visual impairments. For example:

An image about a cat is tagged with alternative text "A cat staring into the night sky";
An embedded speech recording tagged with alternative text of its speech content.

"Actual text" (also called "replacement text") is used for entering textual replacements for images and other items that do not translate naturally into text, or for textual content that is represented in a non-standard manner. This is used to by screen readers to describe the element as a replacement description when applied to text. For example:

An acronym can be tagged with an actual text of its expansion;
A link with text of http://www.example.org could be tagged with "An example web site".

In the SI Brochure, we embed the following content in these tags:

human-readable math markup in alternate text (PDF "Alt"), and
MathML in actual text (PDF "Actual Text").

Both Adobe Reader and Adobe Acrobat Pro can read the content of alternate text via the “Read Out Loud” function (available at the menu bar “View > Read Out Load”).

Adobe Acrobat Pro has additional features to inspect alternate text and actual text tags:

open the "Accessibility" pane, click on "Set Alternate Text" and navigate through entries to see alternate text.

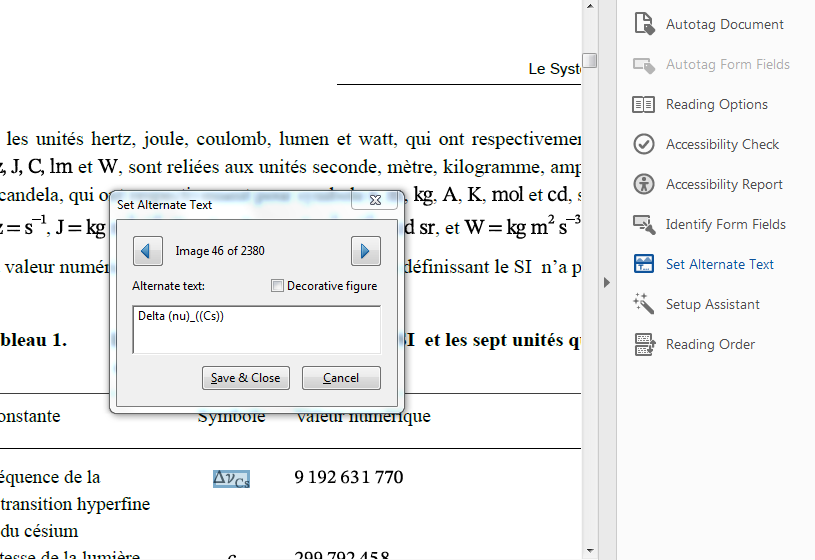Figure 7. View 'Alternate Text' via the Adobe Acrobat Pro "Accessibility" pane
open the “Tags” pane via the menu bar "View > Show/Hide > Navigation Pane > Tags", then manually drill down to the document structure, then right-click the object, then "Object Properties", in order to see the Actual Text and Alternate Text

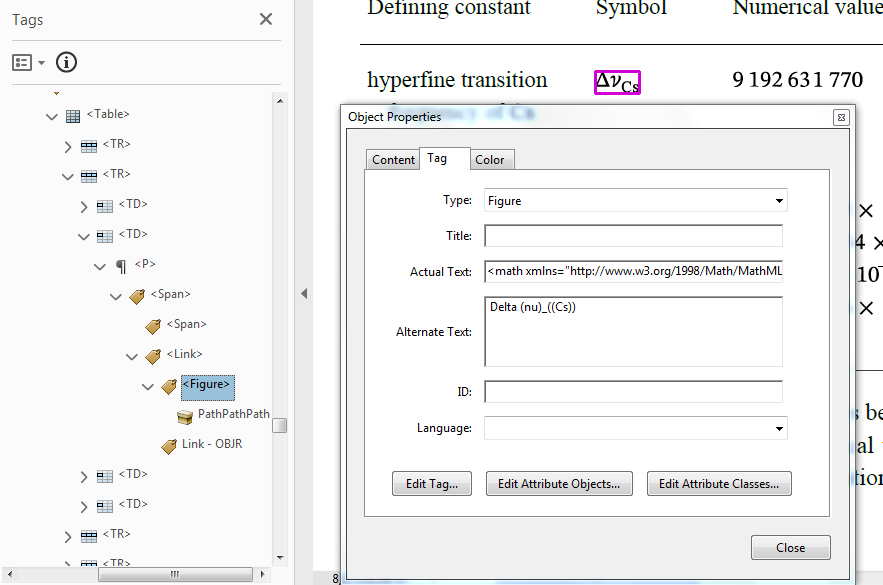Figure 8. View 'Actual Text' and 'Alternate Text' via the Adobe Acrobat Pro "Tags" pane

These accessibility features are essential for visually impaired readers and satisfy accessibility requirements that many organizations face with, including the US government’s Section 508 and the principles described in Techniques for WCAG 2.1 in PDF.

Note	Users without screen readers and accessibility tools may not be able to inspect the implementation of these additional PDF accessibility features.

Table 3. Alternate text and actual text support in PDF readers on different platforms
Support	Platform	Application
✓✓	Windows	Adobe Acrobat Pro (text to speech, alternate text, actual text)
✓	Windows	Adobe Reader (only text to speech)
✓✓	macOS	Adobe Acrobat Pro (text to speech, alternate text, actual text)
✓	macOS	Adobe Reader (only text to speech)
✗	macOS	Preview
✗	macOS	Skim

Note	Acrobat Reader, and macOS applications Preview and Skim, do not have a way to see alternate text and actual text.

Summary

This post demonstrated several cutting-edge techniques in making math formulas accessible in PDFs generated by Metanorma.

While we have used the BIPM SI Brochure as example, these features are supported by all Metanorma flavors out of the box today.

Metanorma users can be confident that their documents will provide the best math accessibility to an audience using any of the major PDF readers.

If you have any further ideas or feedback regarding math accessibility, please do not hesitate to contact us!

References

ISO 32000-1:2008, the PDF 1.7 standard
ISO 14289-1:2014, the PDF/UA (PDF universal accessibility) standard